Fenegyerek fecseg

Az ősi Indiában a tudományos ismeretek nagy része a Védákból származott. A matematika már Kr. e. 2500-ban nagyon fejlett volt. A nulla és a tizedesvessző használatának rendszerét is indiai matematikusok fejlesztették ki. Az asztronómia tudománya például a korabeli, rendkívül bonyolult algebrát használta. Az Kr. e. 2000 körül írt Szúrja Sziddhánta, amely a bolygók tudományával foglalkozó csillagászati könyv, gyakorlatilag a trigonometria és a geometria teljes rendszerét alkalmazza számításai során. Az asztronómia tudományának alapelvei a védikus irodalom bizonyos könyveiben már 5000 évvel ezelőtt megjelentek. Az építészet tudományával (vaszati, vasztu) is külön szentírás, a Silpa Sásztra, illetve a Szthápana Véda foglalkoznak. Már több ezer évvel ezelőtt is voltak megtervezett városok templomokkal, kertekkel, házakkal, palotákkal, mesterséges tavakkal és erődökkel. India templomai között még ma is találhatunk olyat, amely több mint ezer évvel ezelőtt épült. A Dhanur Véda a harcászat tudományáról beszél részletesen, amelyben a fegyverkészítésről és a durva, illetve finom fizikai fegyverekkel történő hadviselés módszereiről esik szó.

Az Ayurveda ősi tudásából merített már az i.e. 4-5. században Hippokratész, majd az i.e. 1. században a kínai gyógyítók (akupunktúra), a 7. században pedig Harun Al Rasid és más arab orvosok, de buddhista szerzetesek közreműködésével az ayurvedikus tudás az i.e. 6. századtól kezdve eljutott Tibetbe, Mongóliába, Koreába és Srí Lankára is, valamint az ókori egyiptomi kultúra gyógyászatára is nagy hatással volt. Az Ayurveda gyógyászati rendszernek a modern kor orvosai, a nyugati (allopatikus) gyógyászat számára is van mondanivalója. Az ősi ayurvedikus szövegekben leírt gondolatok és módszerek fontos kiegészítésként szolgálhatnak a modern, nyugati orvostudomány továbbfejlesztéséhez is. Megismerésük rendkívüli jelentőségű az egészségmegőrzés és a legkülönbözőbb betegségek hatékony gyógyítása és utókezelése szempontjából.
Bár az Ayurvedának igen kifinomult módszerei vannak a legkülönbözőbb betegségek gyógyítására és utókezelésére, mégis elsősorban a betegségmegelőzést, vagyis az egészségmegőrzést tartja szem előtt – hiszen sokkal könnyebb és jobb valamit megelőzni, mint a már kialakult (és esetleg krónikussá vált) problémát kezelni. Az Ayurveda azt vallja, hogy testünk minden porcikájára folyamatos figyelmet kellene fordítanunk még akkor is, ha az éppen tökéletesen egészséges, hiszen csak így őrizhetjük meg hosszú távon egyes szerveink és egész szervezetünk egészségét és épségét.

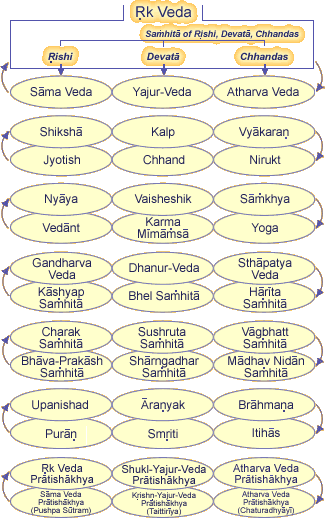
Maharishi Mahesh Jógi azt tanítja, hogy a Véda maga a tudat, az „önmagának suttogó egyesített mező.” A Véda nem csak polcon lévő könyvek sora, hanem magában a tudatban létezik. Mint mondja, ha valaki pusztán a könyvek alapján próbálja felfogni a Védát, akkor igyekezete „merő zűrzavar” lesz csupán. A Véda szanhitá és bráhmana részei annak kifejeződései, ami a tudatban létezik. Minél jobban ismeri valaki a tudatot, annál jobban ismeri a Védát.

Maharishi azt mondja, hogy a Védikus himnuszok olyanok, mint a természettudományok képletei: teljes képet nyújtanak a természeti törvényről, annak különböző értékeiben. Maharishi szerint ahogyan az ember tudatának tisztasága növekszik, úgy tárul fel előtte egyre több a szövegek rejtett jelentéséből. A Véda himnuszai azokat érintik meg a legmélyebben, akik a legközelebb vannak a megvilágosodáshoz. Maharishi úgy tekint e himnuszokra, mint rendkívüli műalkotásokra, melyeket annál inkább képes értékelni valaki, minél tisztább a saját tudata. Minél egyszerűbb tudatosságban vagyunk megalapozódva, mondja, annál többet fogunk fel a Védából.

A Védák irodalmában a Sankhya-filozófia elmagyarázza az univerzum állandó jellemzőinek ismeretelméleti tudásanyagát. E művek olyan tudósokat is megihlettek a múltban, mint Schrödinger, Max Planc, M. Bohr Nóbel-díjas fizikusok a kvantummechanika megalapítói és mások. Témakörük felöleli az egész univerzum ismeret anyagát, többek között annak teremtéséről és elpusztításáról, valamint ami a legizgalmasabb, az univerzum jelenlegi állapotának természetéről is. A modern matematika, fizika, biológia és kémia megismert törvényei mind megtalálhatóak bennük. A Védák a modern tudomány felfedezéseit megelőzve, például megfogalmazzák az energia átalakulásának elvét.

Ugyanezt a tényt erősíti meg az is, hogy olyan hatalmas számokkal tudtak műveleteket végezni, amikre a legtöbb kultúrában sokáig még szavak sem voltak.